Temperature and Rate Indentation Size Effect (TRISE)
and Variable Material Length Lcale
The classical continuum plasticity only predicts a constant hardness and it is unable to predict the size dependency. However, strain gradient plasticity which is based on introducing the gradient in the constitutive relations has been able to account for such micro-structural interaction in order to describe these size effects. In this area, an attempt has been made to determine the variable material intrinsic length scale that scales with strain gradient using stress-strain behavior from macroscopic scale as well as information from micromechanical tests. It is shown that the gradient plasticity theories have given reasonable agreement with the aforementioned size dependence encountered in micro- and nanoindentation experiments.
Using the gradient theory and crystal plasticity, an expression that describes the hardness as a function of indentation depth can be derived. Combining this expression with the outcomes of nanoindentation experiments of a material allows one to determine the value of the material’s intrinsic length scale. In this regards, a physically based model with Temperature and Rate Indentation size effects (TRISE) for single and polycrystalline metals is derived. This model is also able to capture the hardening/softening effect encountered in the polycrystalline materials by considering the effect of the grain boundary. Moreover, the variable material length scale parameter for gradient isotropic hardening plasticity is identified through calibrating the physically based model of the length scale using nanoindentation experiments.
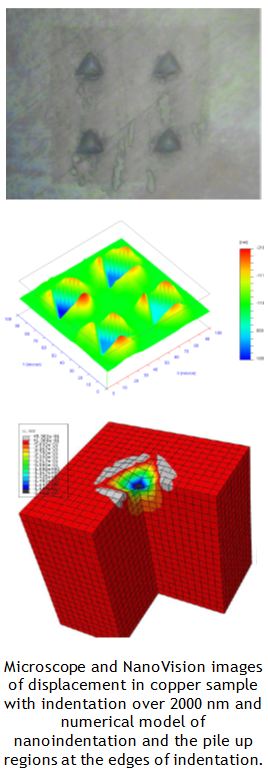
The proposed models are investigated in order to capture the behavior of the materials for different grain sizes (or the distance of indenter from grain boundary in the coarse grained metals), accumulated plastic strains, rates of strain and various temperatures. Results from nanoindentation experiments on different single and polycrystalline FCC, BCC, and steel alloys for various strain rates, and different distances from the grain boundary are used to evaluate the proposed length scale. In order to obtain this variation of accumulated plastic strain with indentation depth for different materials, finite element analysis is performed for the indentation problem. In this regard, the proposed viscoplasticity constitutive model is implemented in the commercial finite element program ABAQUS via a user’s material subroutine coded as VUMAT including the radial return algorithm.
The proposed physically based model gives good predictions for the length scales in metals. These models are used within a wide range of accumulated plastic strains. The proposed length scale is shown to decrease significantly with the accumulated plastic strain. At high strains the length scale tends to zero, corresponding to the local plasticity theory. It is noted also that the length scale increases with the increase in temperature and grain size (distance from grain boundary) and decreases with the increase in strain rate. In general, it can be concluded that the harder materials have smaller values of length scales, Therefore, the indentation size effect is expected to be affected by both prior dislocations and additional work hardening that takes place during indentation. Also, it has been shown that the effect of the grain boundary is only prominent in the first stage of loading, where the boundary can obstruct the movement of GNDs. After overcoming this barrier, the length scale will be the same at higher plastic strains.