Thermo-Mechanical Strain Gradient Plasticity
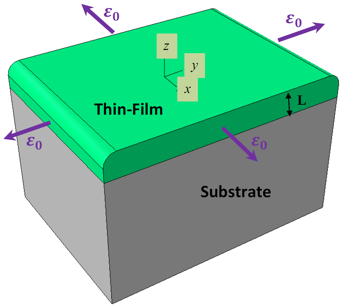

Our current efforts consist of multiscale modeling of the mechanical and thermal properties of materials, with size scaling from nanometer to millimeter, and time scaling from picosecond to minute. The generalized thermodynamically consistent frameworks are developed based on the both phenomenological and physically based yield functions to investigate the thermo-mechanical behavior of the metals in small scale and fast transient time.
In this regard, an enhanced gradient plasticity theory is coupled with the application of micromorphic approach to the temperature variable. In order to account the effect of the multiple sources of thermodynamic processes into modeling and better describe thermodynamic formulations consistently, the mechanical state variables are decomposed into energetic and dissipative components with the corresponding dual parameters for energetic and dissipative gradient length scales. Energetic stresses are defined as the work conjugates of the plastic strain and its gradient while the dissipative thermodynamic forces are defined as the work conjugate of the rate of the plastic strain and its corresponding gradient. The temperature is also included in both the energetic and dissipative state variables.
The corresponding effect of the material microstructural interface between two materials is also incorporated into the formulation. This has been done by assuming either the continuity or the jump of the conjugate’s higher order stresses on both sides of the interface. This leads to two additional material length scales for the interface. On the other hand, the effect of the higher order temperature gradient on the diffusion of atoms and the energy exchange between electrons and phonons are considered using the micromorphic approach. In this regard, two additional time scales are included into the framework which account for the microstructural interactions and the effect of fast transients.
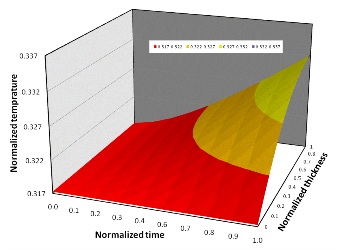
Application of the proposed theories to thin films on thick substrates for various loading conditions and torsion of thin wires are investigated together with the appropriate length and time scales effect on the mechanical and thermal behavior of these structures. The results for the nonlinear ordinary differential equations are obtained numerically and are then compared with the experimental data obtained from various tests.
The next step in this research area is implementing the developed gradient theory to a Finite element code. The proposed formulation will be written in the user material subroutine of ABAQUS finite element software. In order to address the gradient term as an additional degree of freedom, user element should be taken into account.