Theoretical and Experimental Determination of Variable Length Scales
Professor Voyiadjis has dedicated tremendous effort in pioneering the establishment of a consistent formulation and experimental verification of length scales in metals and soils. The definition and magnitude of the intrinsic length scale are keys to the development of the gradient plasticity theory that incorporates size effects. However, the full utility of the gradient-type theories hinges on one’s ability to determine the intrinsic material length that scales with strain gradients, and this study aims at addressing and remedying this situation. Based on the Taylor’s hardening law, a micromechanical model that assesses a nonlinear coupling between the statistically stored dislocations (SSDs) and geometrically necessary dislocations (GNDs) is used here in order to derive an analytical form for the deformation-gradient-related intrinsic length-scale parameter in terms of measurable microstructural physical parameters. This work also presents a method for identifying the length-scale parameter from micro- and nano-indentation experiments using both spherical and pyramidal indenters. The deviation of the Nix and Gao (1998) and Swadener et al. (2002) indentation size effect (ISE) models’ predictions from hardness results at small depths for the case of conical indenters and at small diameters for the case of spherical indenters, respectively, is largely corrected by incorporating an interaction coefficient that compensates for the proper coupling between the SSDs and GNDs during indentation. Experimental results are also show that the ISE for pyramidal and spherical indenters can be correlated successfully by using the proposed model.
However, a fixed value of the material length-scale is not always realistic and different problems could require different values. Moreover, a linear coupling between the local and nonlocal terms in the gradient plasticity theory is not always realistic and that different problems could require different couplings. This work addresses the proper modifications required for the full utility of the current gradient plasticity theories in solving the size effect problem. It is shown that the current gradient plasticity theories do not give sound interpretations of the size effects in micro-bending and micro-torsion tests if a definite and fixed length scale parameter is used. A generalized gradient plasticity model with a non-fixed length scale parameter is proposed by Voyiadjis and his group. This model assesses the sensitivity of predictions in the way in which the local and nonlocal parts are coupled. In addition a physically-based relation for the length scale parameter as a function of the course of deformation and microstructural features is proposed. The proposed model gives good predictions of the size effect in micro-bending tests of thin films and micro-torsion tests of thin wires.
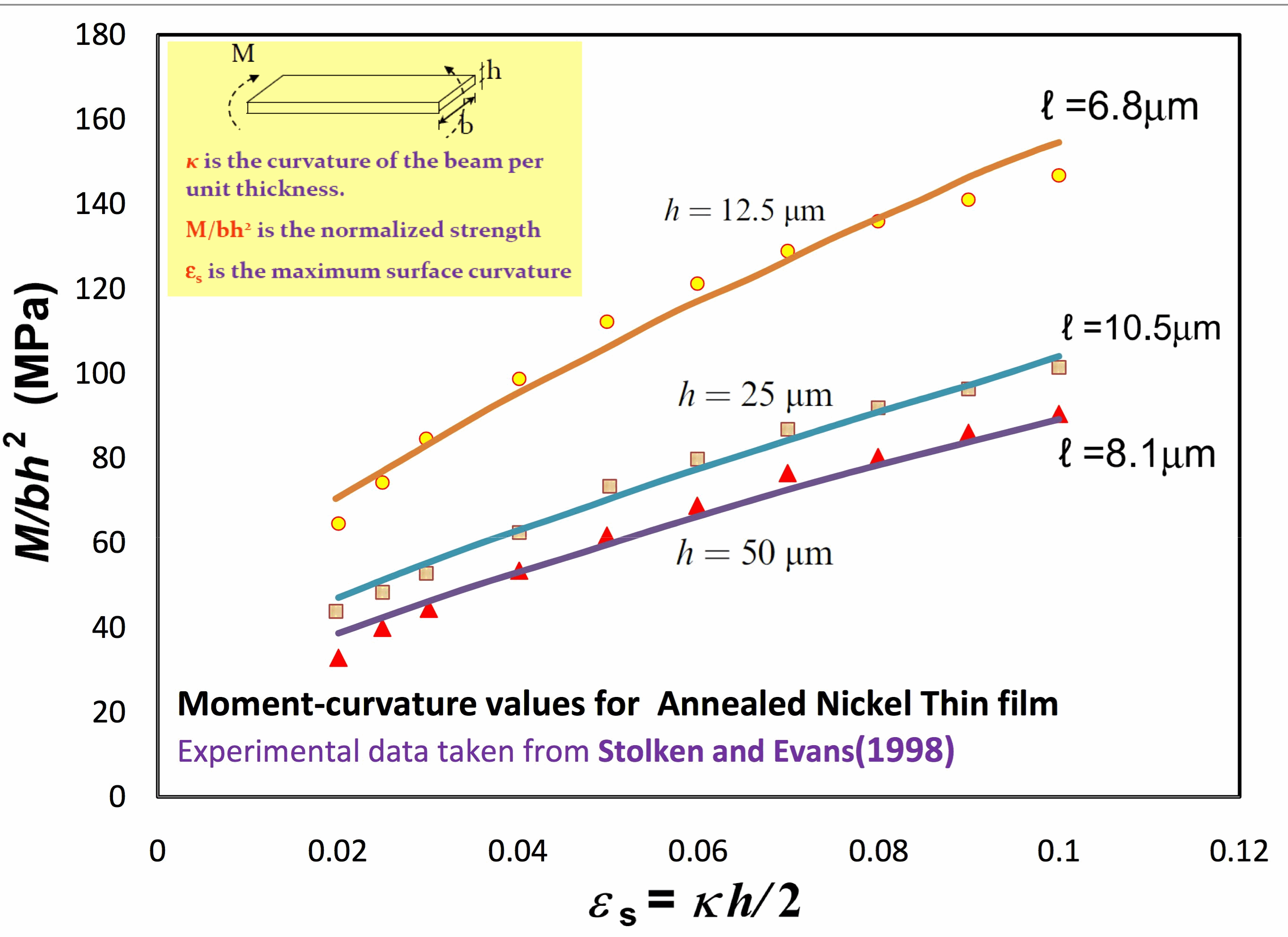
This chart shows the size effect and material length scale for
micro-bending of thin films.
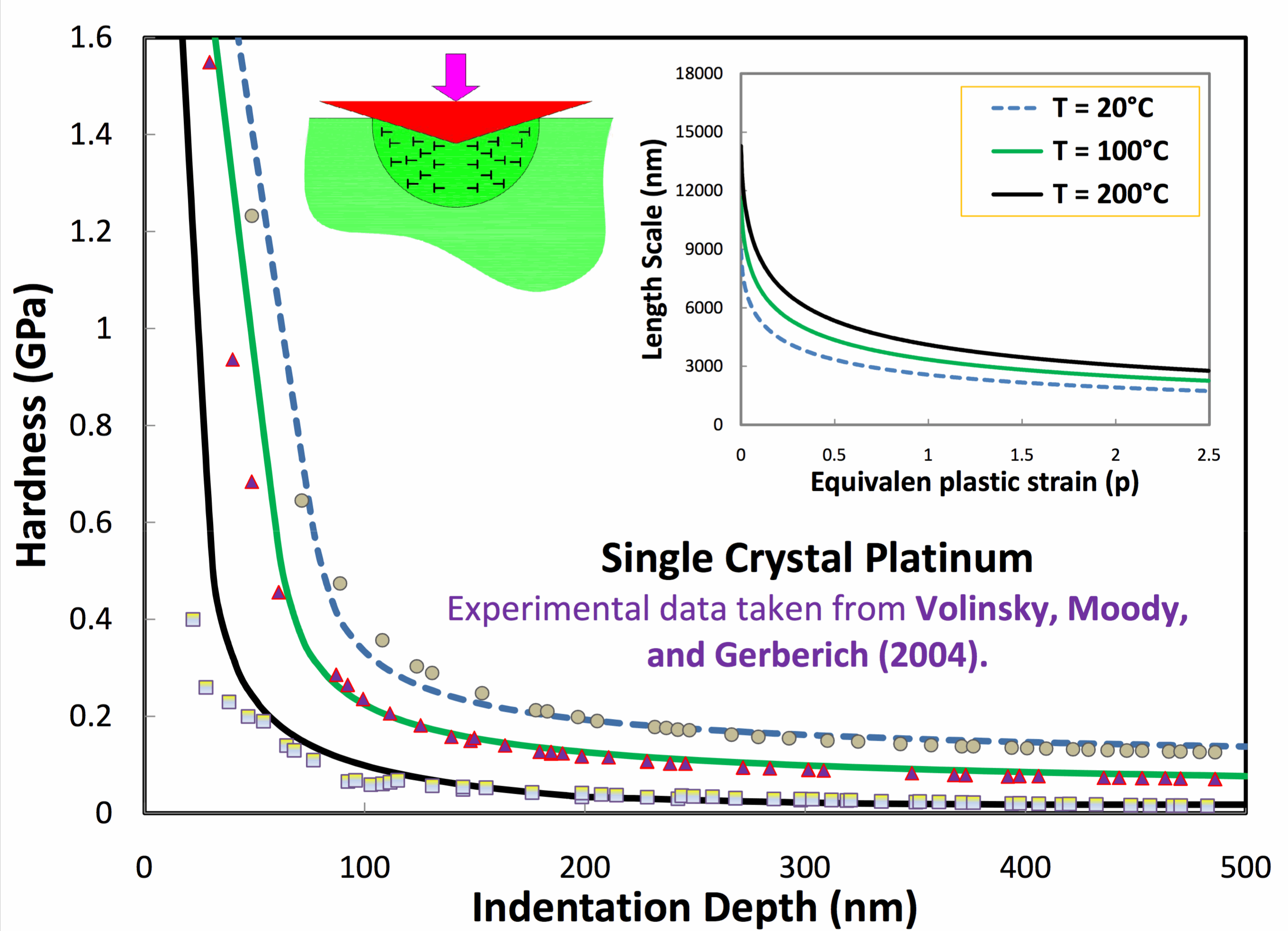
This chart shows the temperature and rate
indentation size effect and variable material length scale.
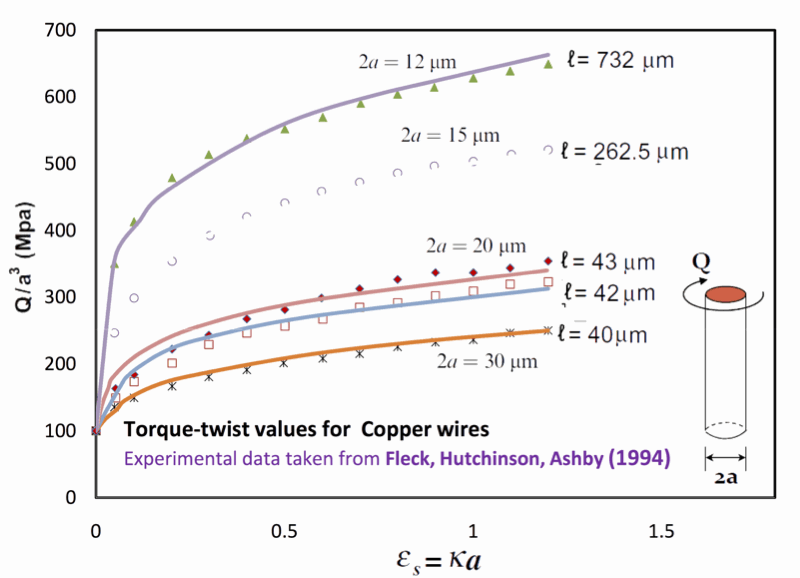
This chart shows the micro-torsion size effect
and material length scale.
Material length scales are also obtained by the Voyiadjis group that is based on experimental observations for metals using nano indentation experiments. A fixed value of the material length-scale is not always realistic and different problems under various conditions could require different values. Therefore, two models are proposed by Voyiadjis and his group for dynamic length scale that depends on strain rates and temperature. The first model is physically based, with parameters related to dislocation densities. This model introduces strain rate and temperature dependency in a coupled form. The second model is a phenomenological one that is based on hardness tests. Both models show that length scale decreases with increasing equivalent strain rate. Very good correlation with experiments is obtained when using these length scales in simulating solutions for high impact energy and perforation problems. Voyiadjis’ group contributions include among others:
- the formulation of higher-order boundary conditions especially, at interfaces, grain, or phase boundaries,
- framework for the formulation of these additional boundary conditions,
- microlevel significance and nature of these boundary conditions is emphasized for biaxial loading of a film-substrate system, in which the material is initially homogenous, that in the absence of the higher-order boundary conditions, the material would support uniform fields and hence the constitutive gradient-dependence would have no influence,
- solutions are obtained in thin films for both constrained and unconstrained plastic deformation at a boundary by employing a simplified form of the constitutive equations,
- clearly indicated that size effect in thin films can be attributed to both the grain size refinement (i.e. Hall-Petch effect) and the film thickness reduction,
- investigated the role of grain size effect on the mechanical behavior of thin films of various thicknesses and thin wires of various radii, where it is shown that the material length scale depends on the mean number of grains across the film thickness or the wire radius, which greatly agree with the experimental observations of Espinosa et al. (2004).
Professor Voyiadjis has been invited by World Scientific Publishing Co. to write a book on nonlocal continuum and length scales:.
Voyiadjis, G. Z., and Abu Al-Rub, R. K., Nonlocal Continuum Damage and Plasticity: Theory and Computations, 610 p., World Scientific Publishing Co., Singapore, (to appear in 2009).